Before working on AI Alignment, I completed a PhD in math (Geometry/Dynamical Systems). This post provides a concise summary of my thesis.
Translation surfaces, other than the torus, possess singularities that can be thought of as points of concentrated negative curvature. My thesis investigated the implications of this intuition and demonstrated that several theorems for negatively curved surfaces have natural analogs in the context of translation surfaces.
My PhD supervisor was Mark Pollicott.
Results
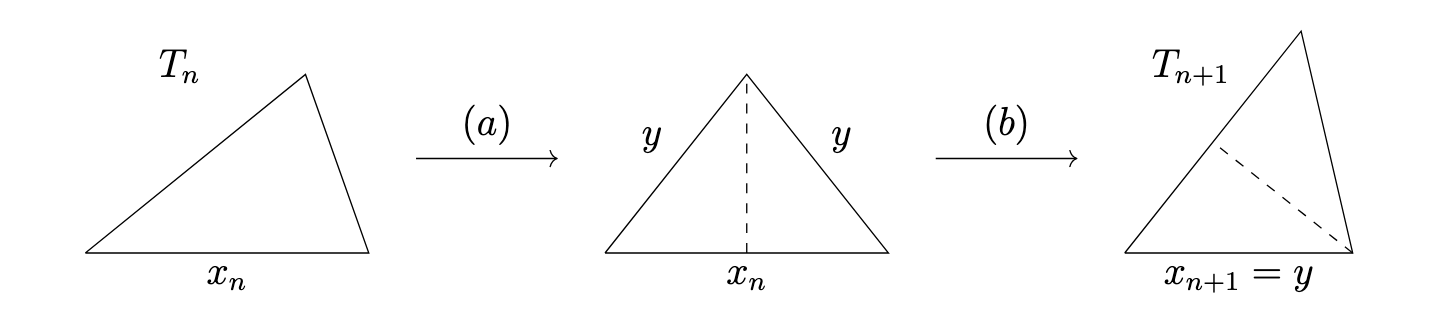
Kneading triangles converge to equilateral triangles
We begin with a fun result that was trying to be a Lemma for the result that follows. Various iterative algorithms can be applied to a triangle to create a sequence of triangles, such as constructing a new triangle by connecting the midpoints of the edges of the previous triangle. It has been proven that many of these algorithms converge to equilateral triangle, regardless of the initial triangle used. We introduce a new triangle algorithm (see below) and show that this algorithm also has this property. Try the interactive visualization here.
Equilateral triangles minimize entropy
Amongst negatively curved surfaces of a fixed area, the surfaces that minimize volume entropy are those that are the most symmetric (those that admit a hyperbolic metric). We show that among certain natural sets of translation surfaces, those that can be tessellated by equilateral triangles have the lowest entropy. This can be considered a demonstration of a "universality phenomenon", where equilateral/hexagonal structures commonly appear as the optimal solution in various minimization problems, such as in beehives, particle configurations, and circle packing. We suspect that a more general result holds.
A prime number theorem analogue for closed geodesic on translation surfaces
The well-known Prime Number Theorem gives an asymptotic formula for the number of prime numbers smaller than a given bound. A similar formula also applies to the number of closed geodesics of length less than some bound on negatively curved surfaces. Alex Eskin presented a talk showing that an analogous formula also applies to translation surfaces (joint work with Kasra Rafi), and we provided a written proof.
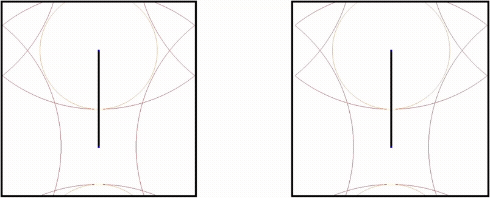
The distribution of large circles on translation surfaces
It has been established that on a negatively curved surface, as the radius of a circle increases, the circle becomes distributed in a natural way. We show that an analogous result applies to "circles" on translation surfaces, despite the unusual fractal shape of these circles.